The reason is because most of the charts we see are flat. In the 16th century, a Flemish geographer named Gerardus Mercator came up with the world’s first orthormorphic chart. In an orthormophic chart, the change in scale across north-south and east-west remains the same, or the rate of change of the scale remains constant. This type of chart became what we now know as Mercator projections. The biggest advantage of a Mercator chart is that all the meridians are distanced same on the chart. This means, if you plot a line on the chart, it will cut the meridians at the same angle at all the points. We call this type of line a Rhumb line. If you want to navigate using such a chart, from let us say position A to position B, you just have to draw a line from A to B and use a protractor to get the track. This track will remain the same until you reach your destination.
The early navigators really liked it, because they had only one track angle to worry about throughout the trip. And with their basic navigation equipment, it made life a little easier. Rhumb lines has a huge disadvantage though. And that is, because the earth is a sphere and not flat, the rhumb line does not give you the shortest distance. If you want the shortest distance you will have to travel on a Great circle track. The easiest way to imagine a great circle is to imagine a ball and placing a piece of string over its surface. If you pull the string on it, that string represents a great circle track. The advantage of navigating a great circle is that it is the shortest distance between two points on a spherical object like the earth.
Now, I hope you get the idea. Airplanes fly great circle routes rather than rhumb line routes. This is because, it makes the trip shorter, making it more efficient. Unlike the rhumb line, the great circle changes its track at every meridian. This is because, on earth from the equator up the pole, the meridians converge changing the track angle. You can simply calculate this convergence by using the formula:
Convergence = change in longitude x sine mean latitude
Below is a solved example. As you can see, from 36N 015 E to 42N 007E there is track difference of 5 degrees. These days all these calculations are done by onboard computers with pin point accuracy. Unlike the navigators back in the day, flying a great circle route presents little of a problem.
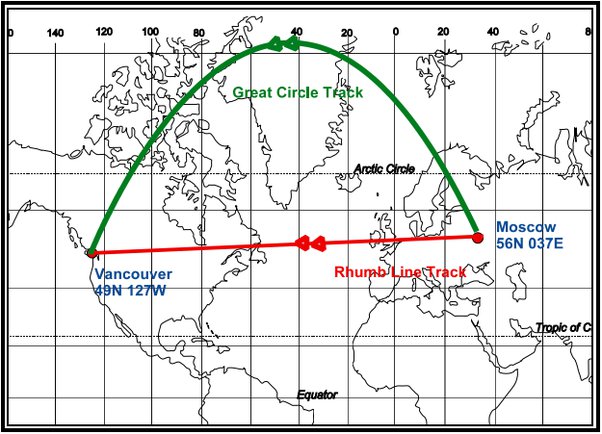
The maps that show airline routes (picture below) are usually Mercator charts and they show curved lines because that is how you represent great circle routes on such a chart. Conversely, the rhumb line is a straight line. Interestingly, on a globe, the great circle route is a straight route while the rhumb line shows a curved path that cuts through all the meridians at the same track angle. However, there is one thing to keep in mind. We do not always fly great circle routes. If an air space is closed or we have to modify our route for some reason like the weather, then we might fly on a longer route which is not the best representation of a great circle from one place to another.
Author – Anas Maaz